ADC 剛好就是亂數產生器嗎？

作者：Nathan Jones

2025-10-22

ADC 有多好？這個問題並非詢問解析度有多少位元；你可能會感到驚訝，一個 16 位元的 ADC 並非一直都提供 16 位元的有用資訊！Mike Stone 在《挑選 ADC》中表示：「許多 16 位元 ADC 實際上是以 7 位元的 ADC 及 9 位元的亂數產生器在運作。」本文將說明如何判斷 ADC 是否產生更多的亂數而非有用資訊，且會介紹幾種簡單的方法來降低隨機性。

試想一個簡化的配置：一個 ADC 在測量光敏電阻上的電壓。如果圖 1 中的 12 位元 ADC (其中 V_FS = 3.3 V) 回報的值為 2048，這是否就表示光敏電阻上的電壓為 1.65 V？

測量光敏電阻電壓的簡化 ADC 設置示意圖 圖 1：測量光敏電阻電壓的簡化 ADC 設置。(圖片來源：Nathan Jones)

不，並非如此！為了示範，我們再取第二個及第三個樣本，或為了實事求是，也可取 100,000 個樣本，然後繪製結果圖。就會看到 ADC 值的分佈 (圖 2)；如果設置沒有任何變動，那麼這些值的任一值都可能真的是光敏電阻上的電壓，其中最值得參考的就是所有樣本的平均值。

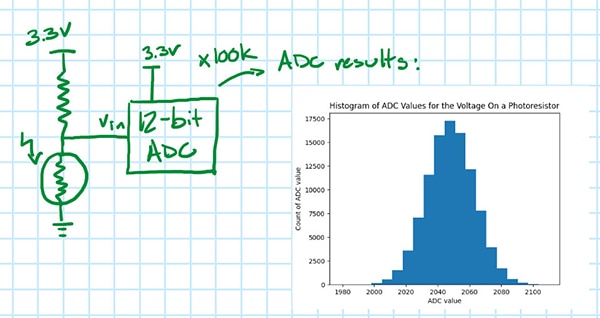圖 2：插圖顯示 100,000 筆光敏電阻電壓樣本的 ADC 值直方圖。(圖片來源：Nathan Jones)

這又會帶出另一個問題。這些變異中是否有部分是輸入訊號中的實際變異？是的，有可能。為了測試，將用已知雜訊位準的電壓參考 (圖 3) 取代電阻分壓器，並重複進行實驗。

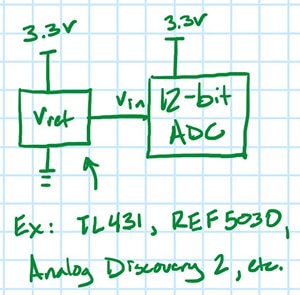使用電壓參考取代電阻分壓器的測試設置示意圖 圖 3：新的測試設置，使用電壓參考取代電阻分壓器。(圖片來源：Nathan Jones)

理想情況下，使用的電壓參考，其雜訊位準應低於 ADC 預期之雜訊位準的三分之一 (例如，若 ADC 預期有 ±1 LSB 的雜訊 [在上述範例中的 ADC 約為 ±0.8 mV]，則理想的電壓參考雜訊位準應低於 0.27 mV_pp)；若符合此條件，則可預期所有測量到的雜訊皆來自 ADC，因為非相關雜訊會以正交方式相加 (參見方程式 1)。

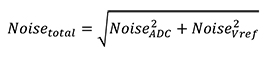方程式 1 [1]

如果 Noise_Vref=Noise_ADC/3，則 Noise_total=1.054× Noise_ADC。這表示電壓參考只佔總雜訊的 5.4%，是可忽略的數值。如果結果顯示電壓參考的雜訊大於 ADC 雜訊的 1/3，記得要從測得的標準差中扣除其佔比 (參見方程式 2)。

方程式 2 [2]

如何得知電壓源的雜訊位準

最簡單的方法就是在規格書上尋找。以下是 Texas Instruments REF5030 規格書的範例，其中指出雜訊位準為 9 μV_pp。

輸出電壓雜訊規格表 圖 4：REF5030 規格書節錄指出輸出電壓的雜訊規格。(圖片來源：Texas Instruments)

如果規格書並未列出雜訊位準 (或只是想確認其數值)，可以使用示波器直接測量，但需先瞭解示波器的背景雜訊。方法是將示波器的一個輸入端接地，並測量觀察到之訊號變動的 RMS 值。圖 5 顯示使用 Analog Discovery 2 (AD2) 進行此操作的結果，並指出 RMS 雜訊約為 0.9 mV。有趣的是，若將時基延長超過 8 µs/div，此值會下降 (降至 µV 範圍)，推測是因為 AD2 採用超取樣與降頻取樣技術來提升其有效解析度。

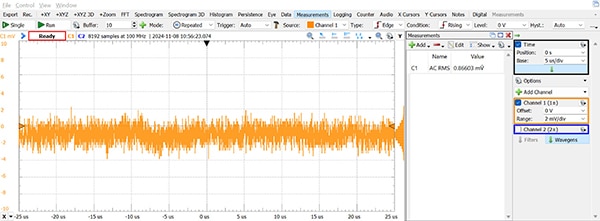圖 5：Analog Discovery 2 示波器的背景雜訊位準圖。(圖片來源：Nathan Jones)

測量電壓源時，示波器訊號的任何變動都是電壓源與示波器兩者雜訊結合的結果。只要那些雜訊來源非相關 (確實如此)，則 Noise_measured=√(Noise²_Scope+Noise²_Vref)，且 Noise_Vref=√(Noise²_Measured-Noise²_Scope)，如上所示。在測量 AD2 產生的 2 V_DC 訊號時，雜訊會判定為 1.2 mV (圖 6)。

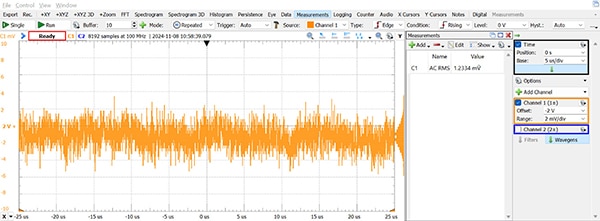圖 6：此 2 VDC 訊號圖指出示波器的雜訊為 1.2 mV。(圖片來源：Nathan Jones)

這表示 AD2 上的訊號產生器亦具有約 0.9 mV 的雜訊。這已經夠低，可用於測試 10 位元 ADC (0.9 mV 剛好小於 3.3 V 滿量程讀數之 10 位元 ADC 的 1/3 LSB)；若是解析度更高的 ADC，測量時必須將此雜訊納入考量。

100,000 筆光敏電阻電壓樣本的 ADC 值新直方圖

圖 7：此插圖顯示出在電壓參考下，100,000 筆光敏電阻電壓樣本的 ADC 值新直方圖。(圖片來源：Nathan Jones)

這樣好多了！請注意第二個直方圖 (圖 7) 的 x 軸僅延伸至 2052 (該圖的分佈 [圖 8] 標準差為 1 LSB)，而第一個圖則延伸至 2100 (其標準差為 15 LSB)。這稱為 ADC 的 DC 直方圖測試，而標準差可有效指出 ADC 中有多少雜訊：每當使用 ADC 測量一個值時，類比引腳上的真實值只有 68% 的機率實際位於該值的 ±1 標準差範圍內，但真實值有 99.7% 的機率位於該值的 ±3 標準差範圍內。

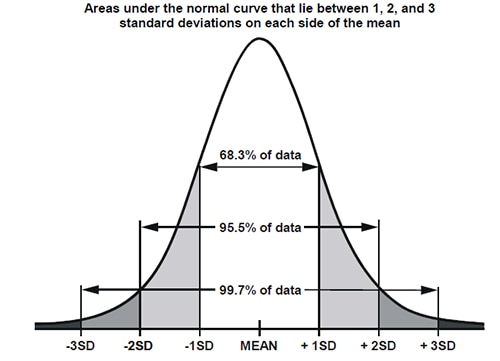標準差的分佈曲線圖 圖 8：標準差的分佈曲線。(圖片來源：https://i.sstatic.net/jkMDV.png)

將此標準差從 LSB 轉換成 V，就可得到 ADC 的輸入參考雜訊 (方程式 3)。

方程式 3 [3]

如果 ADC 的雜訊非常低，以至於所有ADC 代碼全都落在同一個區間，則請嘗試降低 ADC 參考電壓。雜訊位準將保持不變，但會佔用比之前更多的 ADC 代碼，如此就可求得輸入參考雜訊的正確值。

ADC 的有效解析度與無雜訊代碼解析度 (NFCR)代表此雜訊限制 ADC 解析度的程度，計算方法是將 ADC 代碼的完整範圍分割成寬度僅為 1 個 (方程式 4) 或 6.6 個標準差 (方程式 5) 大小的區間。

方程式 4 [4]

方程式 5 [5]

基本上，結果中的實際位元較少，因為 ADC 結果中最後幾個位元出錯或出現雜訊的機率會增加。

DC 直方圖測試有個稍微簡化的版本是將 ADC 的輸入端接地，然後建立 ADC 結果的直方圖 (圖 9)，這與示波器的做法相同。

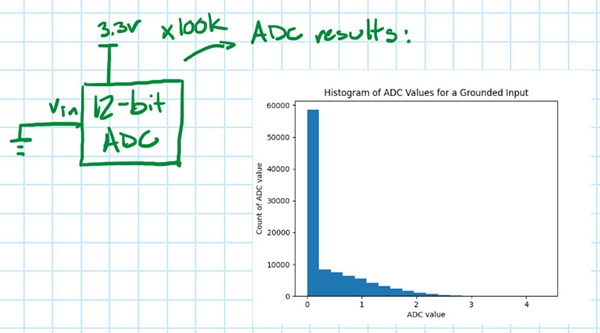輸入端接地下的 ADC 輸出電壓樣本直方圖 圖 9：此插圖顯示輸入端接地時的 ADC 輸出電壓樣本直方圖。(圖片來源：Nathan Jones)

此直方圖的標準差也是 ADC 雜訊的一種測量結果 (排除 ADC 參考電壓所帶來的雜訊，因為不會影響 0 V 的讀數)，但這個數值較低，可樂觀看待。ADC 大概會將低於 0 V 的值回報成 0，因此只會觀察到一半的真實雜訊分佈。在此情況下，如果假設分佈是以其平均值為對稱中心，就可將足夠的中位數值改為負數，讓分佈變得對稱，然後計算該分佈的標準差，就可求得 ADC 雜訊的近似值 (圖 10)。

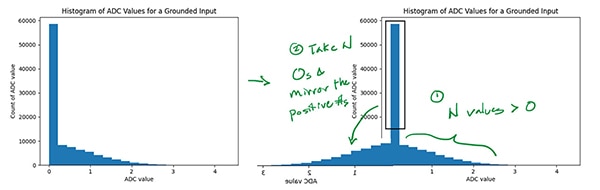圖 10：將圖 9 的直方圖鏡像處理以求得 ADC 雜訊的近似值。(圖片來源：Nathan Jones)

那麼，可針對這些雜訊採取什麼措施？如果 ADC 的解析度仍符合專案需求 (很幸運！)，那麼請記住，每次 ADC 測量都會有一定的不確定性：

比較兩個 ADC 值時，只有在兩個值彼此相差在 6.6 σ 以內 (以達到 99.7% 的比較信心)，或在 σ 以內 (僅有 68% 的比較信心) 時，才視為等值。
在比較 ADC 值與臨界值時，在臨界值比較值上加入一些遲滯 (類似恆溫器的做法)，以免嵌入式系統因雜訊而在臨界值上下反覆觸發。

如果發現 ADC 不再符合專案需求，有一些簡單的方法可以嘗試，以提升效能。在硬體方面包括：

針對 AVCC 和 AREF，使用較低雜訊的參考 (如 Texas Instruments REF5030 或 EVVO TL431)
確保 PCB 上的類比與數位訊號之間僅有最小的串音
在 ADC 轉換期間關閉 CPU (如果 MCU 有支援)，以減少數位雜訊

在軟體端，輸入訊號可以進行超取樣 (即取 N 個樣本的平均值) 以減少雜訊，雖然這會明顯降低最高取樣率。(事實上，有種稱為「超取樣與降頻取樣」的技術可以用來提升 ADC 的解析度，其提升幅度與輸入訊號的超取樣次數相關！)

假設初始設置的 DC 直方圖測試的標準差為 1 LSB。若 ADC 讀數為 2048，現在是否表示 (有 68% 的機率) 真實值為 1.650±0.008V (圖 11)？

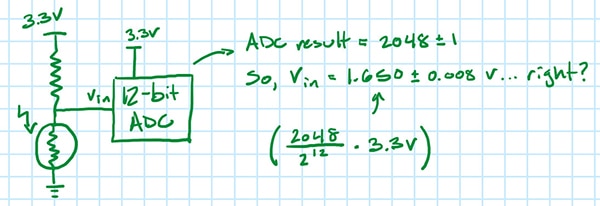真實輸入電壓是否為 1.650±0.008V？的示意圖 圖 11：假設圖 1 設置中的標準偏差為 1 LSB，且 ADC 輸出為 2048，則真實輸入電壓是否為 1.650±0.008 V？(圖片來源：Nathan Jones)

接近了，但仍然不是！這是因為所有 ADC 在測量某個頻率下快速變化的輸入訊號時，都會遇到困難，導致測量不精確 (即產生雜訊)。令人驚訝的是，會發生此情況的頻率可能遠低於 ADC 的最大取樣率！這表示具有 1 MSPS (每秒百萬個樣本) 採樣率的 12 位元 ADC，在輸入訊號接近 500 kHz 時的解析度可能實際上沒有達到 12 位元；當輸入訊號頻率如此高時，ADC 的解析度可能會降至 6 位元或更低。如果嘗試測量光敏電阻上超過 10 Hz 的訊號，ADC 實際上可能並未提供 12 位元的解析度。

為了判斷 ADC 在較高輸入頻率下的解析度表現，可輸入一個已知良好的訊號 (這次為正弦波)，並測量 ADC 值與該已知良好訊號的相符程度 (圖 12)。(正弦波「就夠了嗎」？這部分將在測試執行程序揭露後進行討論；如此會更有意義。)

已知良好正弦波輸入的測試設置示意圖 圖 12：已知良好正弦波輸入的測試設置。(圖片來源：Nathan Jones)

為了提供正弦波，可以使用函數產生器 (例如許多 USB 示波器中內建的那種)、DDS 晶片 (如 Analog Devices 的 AD9834) 或可自行組裝正弦波產生器 (以文氏電橋振盪器為基礎，或使用像是 Analog Devices 的 MAX7400 對方波進行低通濾波)。務必注意，在此測試中，僅可使用非取樣頻率整數子倍數的輸入頻率 (例如，若取樣率為 100 kHz，就不應使用 1 kHz 的輸入頻率)。這是為了避免在每個週期的相同位置對正弦波取樣時出錯。此外，為了對 ADC 進行最大壓力測試，請將輸入正弦波的振幅設定成不會讓輸出出現「裁切」的最大值 (例如對於上述範例的 ADC，稍低於 1.65 V)。

在收集 ADC 結果後，將資料擬合成正弦波，以計算殘餘誤差。正弦波擬合幾乎可以使用任何數量的資料進行，但為了獲得最佳結果，輸入正弦波必須至少包含五個完整週期。要開始正弦擬合演算法，可能要先猜測振幅、頻率、相位偏移和偏移量 (圖 13)。

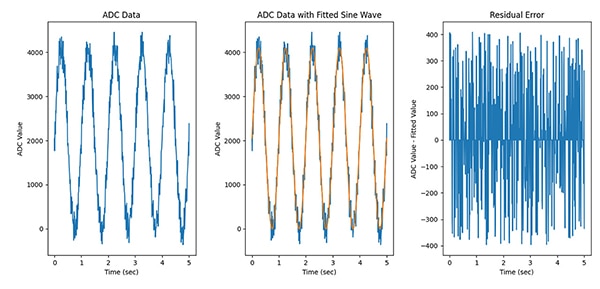圖 13：透過正弦波擬合演算法，就可判斷殘餘誤差。(圖片來源：Nathan Jones)

此測試稱為 ADC 的正弦波擬合測試，殘餘誤差的 RMS 值可用來衡量 ADC 在特定輸入頻率下的雜訊程度。在較低頻率時，RMS 雜訊應與 DC 直方圖測試中的參考輸入雜訊相符，但在較高頻率時，幾乎肯定會因上述那些與頻率相關的雜訊源而退化。

可利用正弦波擬合測試求得的 RMS 雜訊值來計算 ADC 的有效位元數 (ENOB) (方程式 6)，這代表理想 ADC 的位元數，而此 ADC 唯一的雜訊來源是量化雜訊，並具有與 ADC 中雜訊相同的 RMS 值。

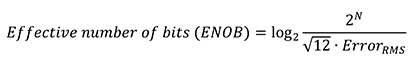方程式 6 [6]

此值僅限於使用之輸入訊號的頻率。為了更全面瞭解 ADC，應重複執行此測試的頻率應一路上升至最高的相關輸入訊號，或上升至最大取樣率的一半。可能會發現，在遠低於最大取樣率一半的頻率下，雜訊會大幅上升 (ENOB 則大幅下降！)。舉例而言，這一系列的測試就在 STMicroelectronics 的 STM32F042K6 ADC 上完成執行並繪製結果 (圖 14)。

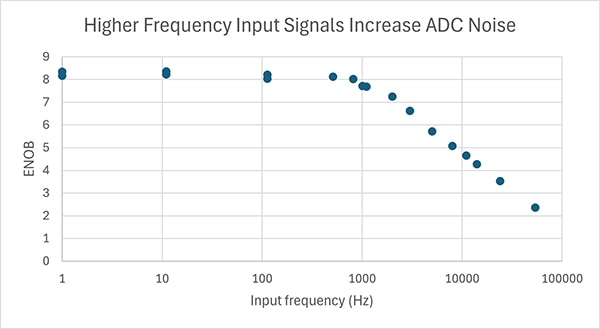STM32F042K6 微控制器中 ADC 的頻率雜訊測試圖 圖 14：STM32F042K6 微控制器中 ADC 的頻率雜訊測試。(圖片來源：Nathan Jones)

雖然 STM32F042K6 微控制器上的 ADC 可在 1 MHz 下取樣，但解析度在超過 1 kHz 時會下降；如果目標是用這個 ADC 來測量 10 kHz 訊號，當時的解析度大約只有 5 位元！(亦請注意，最大 ENOB 約為 8.3；這是因為即使在 DC 下也有大約 10 LSB 的雜訊，會導致 ADC 的有效解析度從 12 位元直接降低到約 8.7 位元。這些測試是在未改裝的 STMicroelectronics Nucleo-F042 開發板上進行；如果使用上述任何技術，結果將會大幅改善。[好啦，可針對這些雜訊採取什麼措施？])

如何得知正弦波的雜訊位準

與電壓參考一樣，如果正弦波的雜訊位準是可直接觀察或推理而得 (即，如果無法在規格書上取得)，那麼就要使用示波器來測量。先前討論的正弦波擬合技術就可用來凸顯正弦波產生器的雜訊。

首先，將示波器的輸入端接地，並計算輸出端的 RMS 值 (如先前「如何得知電壓源的雜訊位準」章節所述)，藉此判定示波器的背景雜訊。
接著，測量正弦波產生器的輸出，將結果擬合成完美的正弦波，並計算殘餘誤差的 RMS 值。然後使用方程式 2 來判定正弦波產生器的雜訊 (以示波器的背景雜訊當作其 AC 雜訊的近似值)。

理想情況下，正弦波的雜訊位準會低於 ADC 預期雜訊位準的 1/3 (換句話說，正弦波是「頻譜純淨」的)，因此其對測得雜訊的佔比可以忽略不計。如果正弦波的雜訊位準高於該值，請記得在計算殘餘誤差的 RMS 值後求得的測得雜訊中將其扣除。

此測試應對每個要用於測試 ADC 的輸入頻率重複進行 (即使正弦波產生器可能也有與頻率相關的雜訊源！)。

可針對這些雜訊採取什麼措施？首先，建議在訊號源與 ADC 之間放置一個低通濾波器 (LPF)，其截止頻率略高於相關的最高訊號頻率，藉此協助限制高頻雜訊 (對任何數據採集系統來說，這通常是「好事一樁」)。如果相關的最高頻率訊號位於 ENOB 與輸入頻率關係圖中的「拐點」以下，則實際上解析度並無任何損失。若要嘗試測量高於該「拐點」的訊號，有嘗試幾個方法來提高較高頻率下的解析度。包括：

確保連接至類比引腳的裝置輸出阻抗非常低，必要時可插入運算放大器進行緩衝。
調整 ADC 時脈或其取樣／保持時間，使其盡可能快速，同時仍讓內部電容有足夠時間充電
使用低抖動的 ADC 時脈來源，並配置系統以固定間隔採集 ADC 樣本

除非以非常窄頻段內的訊號為目標，否則接下來最直覺的作法就是假設實際輸入訊號從 DC 到 LPF 的截止頻率之間具有均勻的頻率成分，因此每次 ADC 測量中的 RMS 雜訊即為使用正弦波擬合測試從 DC 到截止頻率測得的平均 RMS 雜訊。如果希望使用先前討論的 STM32F042K6 來測量最高達 10 kHz 的寬頻訊號，最佳作法是將 ADC 視為每次測量僅有約 6 位元的 ENOB。此值很可能低於使用 DC 直方圖測試所求得的值，這表示若 ADC 測量中有較高頻率成分的可能性，每次測量的確定性將較低。

下一個要考量的假設是在感測器與 ADC 之間加入一個 LPF，如此一來從 DC 到截止頻率的 RMS 雜訊僅有 ±1 LSB。若 ADC 讀數為 2048，現在是否表示 (有 68% 的機率) 真實值為 1.650 ±0.008 V (圖15)？

電路中加入低通濾波器是否會達到 1.650±0.008V 真實值？示意圖 圖 15：在電路中加入低通濾波器是否會達到 1.650±0.008 V 的真實值？(圖片來源：Nathan Jones)

聽起來很瘋狂，但仍未達到！雖然本文已有效地凸顯 ADC 中的雜訊，但尚未呈現其誤差。在本文所述的測試後，唯一可以確定的是兩個 ADC 值是相同還是不同。然而，目前尚不清楚 ADC 代碼 2048 是否確切對應 1.65 V，或是其他數值。增益、偏移和差動非線性誤差 (以及其他因素) 可能都會導致 ADC 代碼轉換成實際電壓的過程比使用 V_in=ADC 結果 × V_FS/2^N 更為複雜。但這會是另一篇文章的主題了！